Robot maths and control
W.S.Harwin
March 2016
Index Next Lecture Previous Lecture- Wheeled machines
- Serial chain linkages
- Control
Coordinate frames
\[ x_{\text{X}w}=x_{\text{X}r}\cos\theta_c - y_{\text{X}r}\sin\theta_c +x_c \] \[ y_{\text{X}w}=x_{\text{X}r}\sin\theta_c + y_{\text{X}r}\cos\theta_c +y_c \]
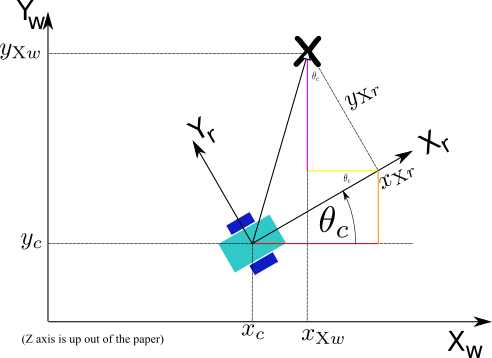
Coordinate frames.
\[ x_{\text{X}w}=x_{\text{X}r}\cos\theta_c - y_{\text{X}r}\sin\theta_c +x_c \] \[ y_{\text{X}w}=x_{\text{X}r}\sin\theta_c + y_{\text{X}r}\cos\theta_c +y_c \] \[ \left[\begin{array}{c} x_{\text{X}w}\\ y_{\text{X}w}\\ 1 \end{array}\right] = \left[\begin{array}{ccc}\cos\theta_c&-\sin\theta_c&x_c\\ \sin\theta_c&\cos\theta_c&y_c\\ 0&0&1\\ \end{array}\right] \left[\begin{array}{c} x_{\text{X}r}\\ y_{\text{X}r}\\ 1 \end{array}\right] \]

Coordinate Frames
Robot to world frame conversion \[ \left[\begin{array}{c} x_{\text{X}w}\\ y_{\text{X}w}\\ 1 \end{array}\right] = {}^w_rT \left[\begin{array}{c} x_{\text{X}r}\\ y_{\text{X}r}\\ 1 \end{array}\right] \] World to robot coordinate frame conversion $$ \left[\begin{array}{c} x_{\text{X}r}\\ y_{\text{X}r}\\ 1 \end{array}\right] = {}^r_wT \left[\begin{array}{c} x_{\text{X}w}\\ y_{\text{X}w}\\ 1 \end{array}\right] = {}^w_rT^{-1} \left[\begin{array}{c} x_{\text{X}w}\\ y_{\text{X}w}\\ 1 \end{array}\right] $$

Two independent wheels


Robot Kinematics of two independent wheels
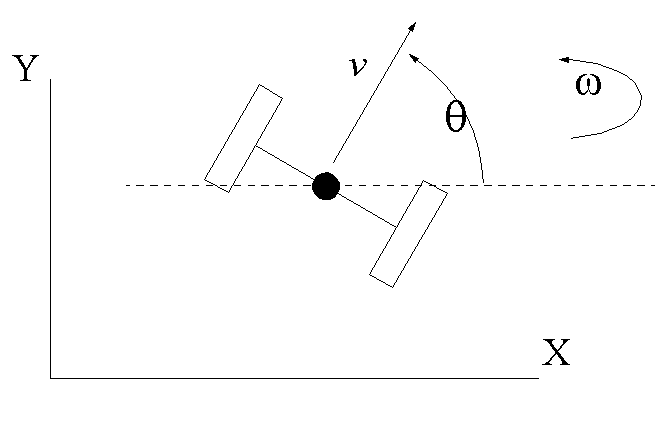
$$v_x=v \cos\theta={dx \over dt}$$ $$v_y=v \sin\theta={dy \over dt}$$ $$\omega={d\theta \over dt}$$
where $v$ is the forward velocity of the robot, angled at $\theta$ to the $x$ axis.
Wheel equations
$$v={(\omega_R+\omega_L)R\over 2}$$ $$\omega={(\omega_R-\omega_L)R\over L}$$
where $R$ is the radius of the wheels and $L$ is the distance between wheels
Forward dead reckoning
- Requires numerical integration techniques
- Usually forward or backward Euler
- Errors accumulate
- Wheel slip
- Inacurate parameter estimates (e.g. for R and L - flat tires?)

Inverse Kinematics
Also known as non holonomic planning Multiple solutions e.g. \[v=3\] $$ \theta=\begin{cases} 0,& \text{if $0\le t<0.4$}\\ \frac{5\pi}{2}\left(t-0.4\right),& \text{if $0.4\le t<0.6$}\\ \frac\pi2, & \text{if $0.6\le t<1$} \end{cases}$$
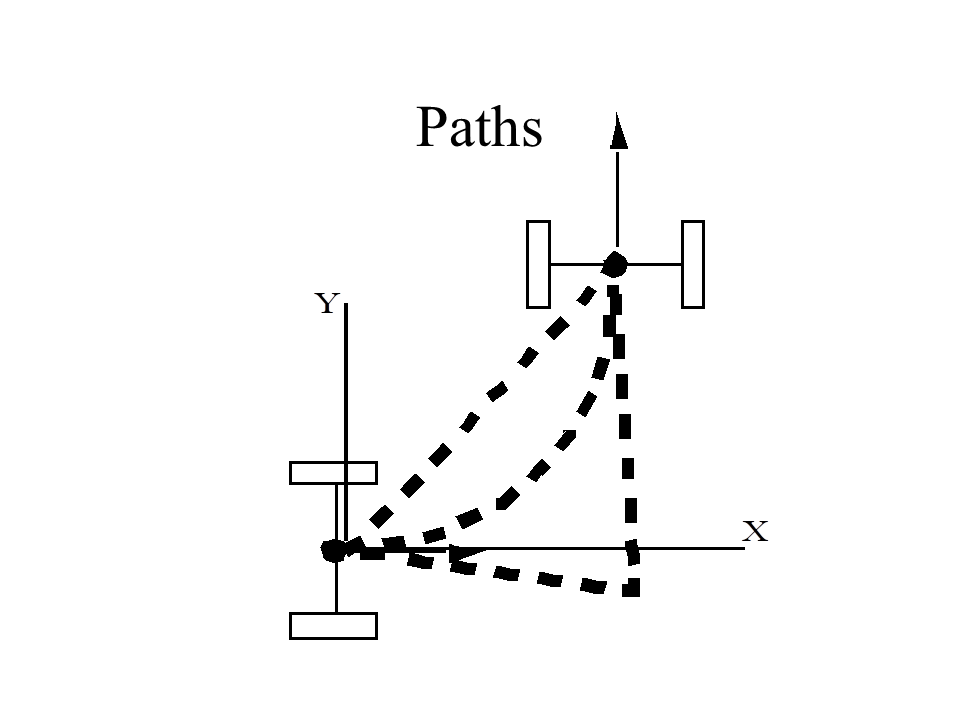
Manipulator Kinematics
- Cartesian robots have simple kinematics
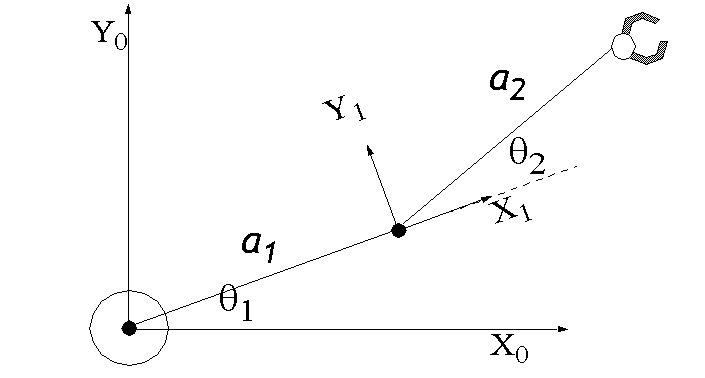
- Consider a planar 2R serial chain robot.
$$x=a_1\cos\theta_1 + a_2\cos(\theta_1+\theta_2)$$ $$y=a_1\sin\theta_1 + a_2\sin(\theta_1+\theta_2)$$ $$\theta=\theta_1+\theta_2$$
Paper
- http:paperrobot paper robot
Inverse kinematics
- Elbow in/elbow out solutions
$$x^2+y^2=a_1^2+a_2^2+2a_1a_2\cos\theta_2$$
| hence |
$$\theta=\arccos\left({(x^2+y^2)-(a_1^2+a_2^2) \over 2a_1a_2}\right)$$
- no solution if the expression is not between $-1$ and $1$.
$$\tan(\alpha+\theta_1)={y \over x}$$ $$\sin\alpha={a_2\sin\theta_2\over \sqrt{x^2+y^2}}$$

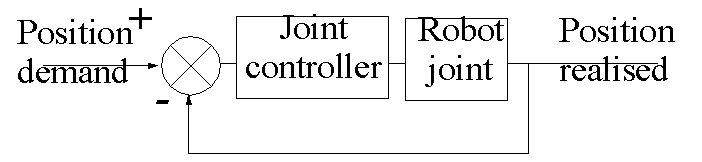
Control