This is an overview of the physics and maths needed to simulate basic Braitenberg vehicles. This can be extended into other vehicles and details are given on Grey Walter's M. Speculatrix and on 'Preditor/Prey' behaviours. The challenge is to extend this behaviour (with realistic physics) to flocking behaviours.
A simulation that should run on windows and linux operating systems is available at http:braitenberg.html Braitenberg vehicles or on github at https://github.com/WSHarwin/Neuron-vehicles
The original monograph was V. Braitenberg, "Vehicles: Experiments in synthetic psychology." [braitenberg1986vehicles], digital versions are available as is a copy in the UR Library as Call 152-BRA.
Grey Walter published his work in a series of articles and books [grey1953living][Walter1951machine][Walter1950imitation]
Objects in the braitenberg world are
Braitenberg robots are either direct gains between the eyemodel and the wheel motors, (excitatory synapse) i.e.
| Motortorque=lightlevel* const1 |
or an inverse gain (inhibitory synapse) of the form
| Motortorque=const1/(lightlevel+const2) -const3 |
Machina Speculatrix drives forward when it sees the light, otherwise it spins
This is used by M. Speculatrix
Used by preditor prey and the Braitenberg Vehicles
Assume a body mass $M$ and inertia $I$.
Assume positive torque drives wheels forward such that positive $\tau_L$ and $\tau_R$ produce forces on the robot in the same direction. If the wheel radius is $r$ then \[f_L=\tau_L/r\] and \[f_R=\tau_R/r\] Thus the total force acting on the CoM (Centre of Mass) of the robot is \[f_L+f_R=\tau_L/r+\tau_R/r=M\ddot{x}\] Rewrite as \[\ddot{x}=\frac{\tau_L+\tau_R}{rM}\] to allow numerical integration.
Likewise the torque acting around the CoM of the robot \[(\tau_R/r-\tau_L/r)\frac{l}2=I\ddot{\theta}\] again rewrite as \[\ddot{\theta}= (\tau_R-\tau_L)\frac{l}{2Ir}\]
Eye model for braitenberg vehicles is Intensity = sum for all lights $\cos(angle\_to\_light)/dist^2$ to light
Locate eyes at x,y,theta on body frame. If ${}^w_1A$ is vehicle (or person) frame in world coordinate frame and ${}^1_eA$ is eye in vehicle frame, then we need to work out the object in eye frame.
Since
\[ {}^w\!x={}_1^w\!A ~^1_e\!A ~^{e}\!x \]
The solution is \[ ~^1_e\!A^{-1} {}_1^w\!A^{-1} ~^w\!x=~^{e}\!x \]
Provided all objects are round and the same size, we can use inverse square law. If round objects are different diameters, the intensity should simply scale the inverse square by the diameter. Thus the 'area' (length) on retina will be $\theta\pm\alpha$ where theta=atan2(y,x), and alpha is object diameter/distance to object
Let $r1$ $r2$ define receptor angle where we can guarantee $r1>r2$ and $o1$ $o2$ define the angles of the edges of the object in the visual field, again $o1>o2$. There are four possible arrangments of the light reflected from the object hitting all or part of the receptor. These are
| $r1>o1>r2>o2$ when the overlap is o1-r2 |
| $r1>o1>^1o2>r2$ when the receptor gets all the light from the object, i.e. o2-o1 |
| $o1>r1>^2r2>o2$ when the light from the object spills over the receptor i.e. r1-r2 |
| $o1>r1>o2>r2$ when the overlap is r1-o2 |
$^1$ and $^2$ are unnecessary tests as they are known apriory.
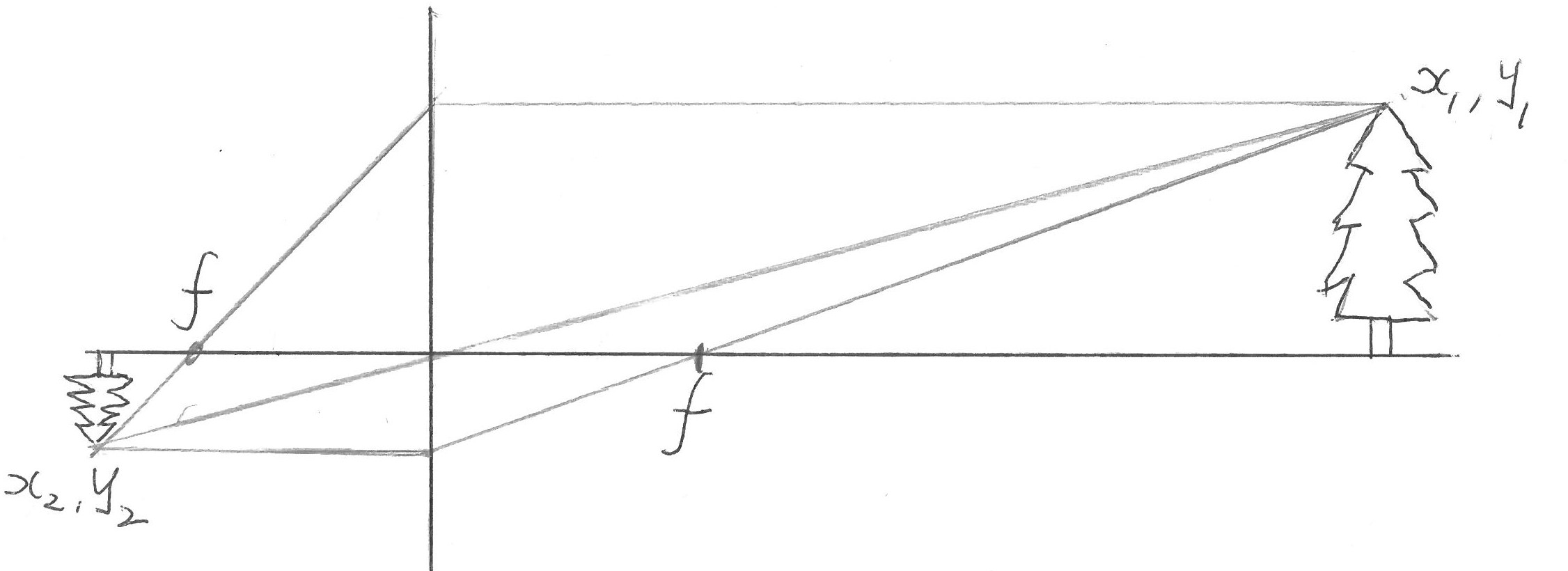 Pinhole camera model (pinhole at the origin)
Pinhole camera model (pinhole at the origin)
[Walter1951machine] W Grey Walter, A machine that learns 1951 url=http://robotics.cse.tamu.edu/dshell/cs643/papers/walter51learns.pdf
[Walter1950imitation] W Grey Walter, An imitation of Life 1950 url=http://robotics.cse.tamu.edu/dshell/cs643/papers/walter50imitation.pdf
[grey1953living] William Grey Walter, The living brain 1953
[braitenberg1986vehicles] V. Braitenberg, Vehicles: Experiments in synthetic psychology 1986 152-BRA url=http://www1.appstate.edu/~kms/classes/psy5150/Documents/Braitenberg1984.pdf