A Robot Teaches Itself How to Walk from swissnex San Francisco
Cognitive Robotics and Artificial Intelligence from swissnex San Francisco
Relates degrees of freedom to the links and joints.
$m=3(n-j-1)+\sum^j f_i$
$m=6(n-j-1)+\sum^j f_i$
where $n$=number of links, $j$= number of joints, $f_i$ = d.o.f. in joint $i$, $m$=degrees of freedom Usually need to have at least one actuator per degree of freedom
Six lower order kinematic pairs
| name | DoF | type |
| Revolute | 1 | R |
| Prismatic | 1 | P |
| Screw | 1 | R+P |
| Cylindrical | 2 | RT |
| spherical/Ball | 3 | RRR |
| Planar | 3 | RRT |
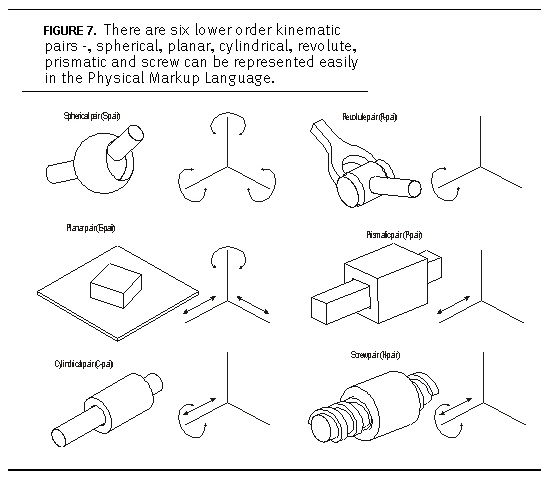
In fact the screw is the most general robot joint. All rigid motion of links in a robot can be described as a combination of screw motions.
Question, how does a screw joint represent


Robot (and human) workspace is limited by
Singularities are where the Jacobian is singular, (in this case the Jacobian is a location dependent relationship beween the joint veolcity and the endpoint velocity) \[ \Delta x=J \Delta\theta \]
So if J is singular, then to achieve a specific $\Delta x$ requires an infinite joint velocity vector.
Likewise \[ \tau=J^T F \] where $\tau$ is the joint torque and $F$ is the end point force so at a workspace singularity there is no ability of the joints to opose the external force
Examples